DL基础理论
DL基础结构单元
卷积层
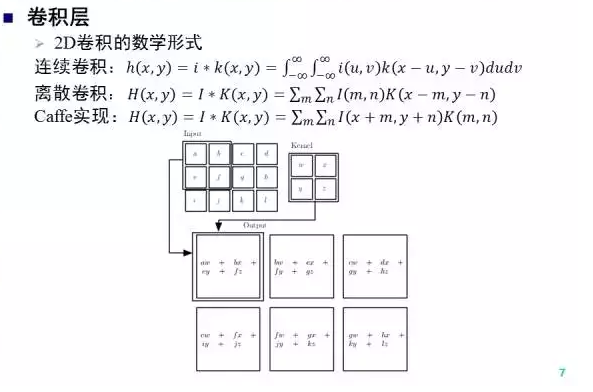
卷积是深度网络的重要结构单元之一。我们给出了2D卷积的连续和离散形式,注意卷积核需要做中心翻转。在Caffe实现中,卷积核假设已经翻转,所以卷积运算可以看作当前窗口和卷积核的一个 内积 (不考虑bias项),上图我们给出了一个卷积运算的示意。
与全连接层相比,卷积层的输出神经元只和部分输入层神经元连接,同时相同响应图内,不同空间位置共享卷积核参数,因此卷积层大大降低了要学习的参数数量。
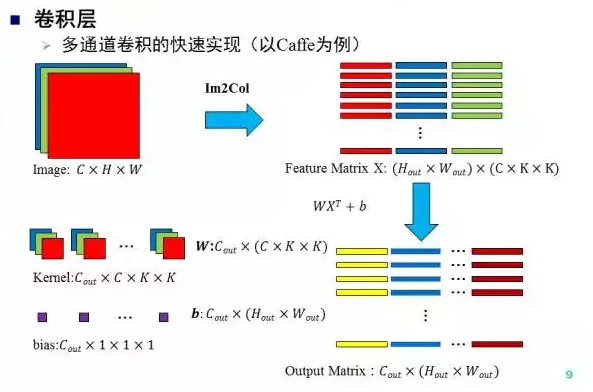
Caffe当中,为了避免卷积运算中频繁的内存访问和过深的循序嵌套,对卷积运算进行了以下加速:通过 Im2Col 操 作一次取出所有的patch并组成矩阵,与kernel矩阵做乘法运算直接得到卷积结果。
特别注意:
例如 alexnet:输入图像是227×227×3(注1),conv1的卷积核参数是:
kernel_size: 11
stride: 4
num_output: 96
因此实际的卷积核维度是11×11×3,channel是输入的图像的第三维(如果是后面的卷积层,其卷积核的channel是与之做卷积的输入的feature map的数量),即3,做卷积的时候,是11×11×3的卷积核和输入图像里的11×11×3的块进行卷积,得到一个值,卷积的过程是在height和width上滑动,第三维上不滑动,因此得到的feature map是二维的
反卷积层
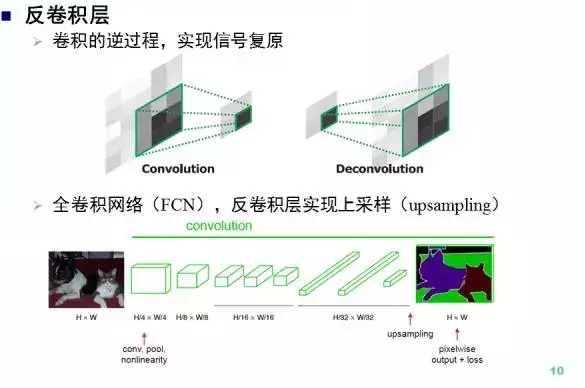
有卷积就有反卷积,反卷积是卷积的逆运算,实现了信号的复原。在 全卷积网络 中,反卷积层实现了图像的上采样,从而得到如输入图像大小相同的输出。
这里 全卷积网络 FCN,主要思想有 CNN的全连接层转换为卷积层和通过反卷积进行上采样。 ,这个值得深入了解,尤其是在end-to-end 像素级的图像理解和图像语义分割
(semantic segmentation 论文 )方面 : 有较好的应用.
其他参考1
其他参考2
pooling层
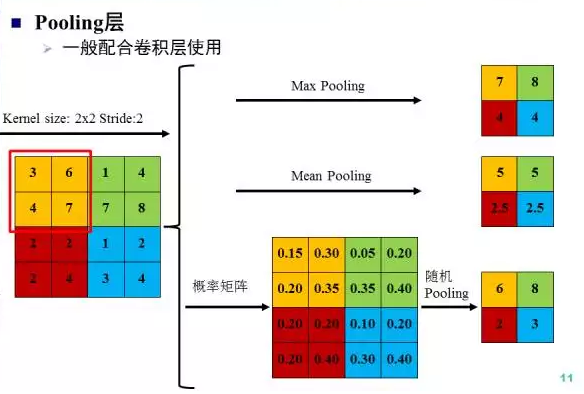
Pooling层一般配合卷积层使用,改变feature map的尺寸,不改变通道数,可以获得特征的不变性。常见的Pooling操作有max pooling、mean pooling和随机pooling。其中max pooling取最大值,mean pooling取均值,随机pooling按响应 值的大小依概率选择。
激活函数
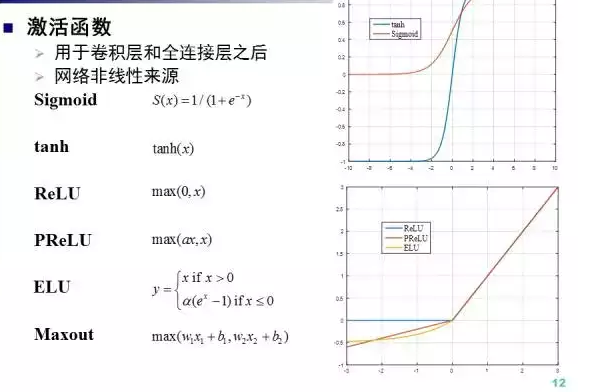
激活函数一般用于卷积层和全连接层之后,激活函数是深度网络非线性的主要来源。常见的激活函数Sigmoid, 双曲正切,ReLU(生物启发,克服了梯度消失问题), PReLU(alpha可学习), ELU和maxout。 其中PReLU和ELU都是ReLU的改进。
Dropout
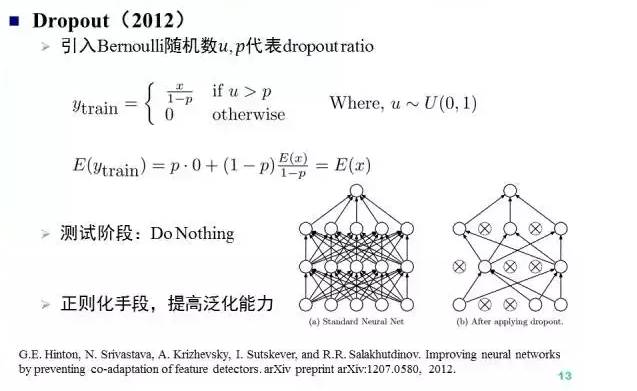
Dropout由Hinton组提出于2012年,Dropout随机将比例为p的神经元输出设置为0,是一种避免深度网络过拟合的随机正则化策略,同时Dropout也可以看作是一种隐式的模型集成。
Batch Normalization
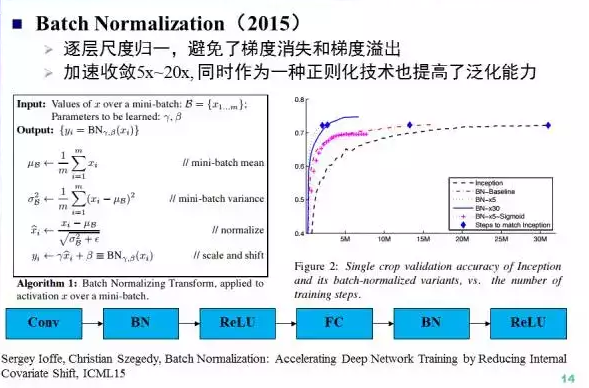
Batch Normalization提出于2015年,通过逐层尺度归一(零均值方差归一,scale和shift),BN避免了梯度消失和梯度溢出。BN可以加速收敛5x~20x, 作为一种正则化技术也提高了泛化能力。论文 知乎
损失函数

用于单标签分类问题的Softmax损失函数,用于实值回归问题的欧式损失函数,用于多标签分类的Sigmoid交叉熵损失和用于深度测度学习的Contrastive损失。
DL训练方法
##### 梯度下降

有了BP算法传递的梯度,基于梯度下降方法,就可以对网络参数进行更新。梯度下降方法的缺点是速度慢且数据量大的时候内存不足,随机梯度下降方法的缺点是方差大导致损失函数震荡严重。两者折中的Mini-batch SGD,我们也给出了基于Mini-batch SGD的NN训练流程。
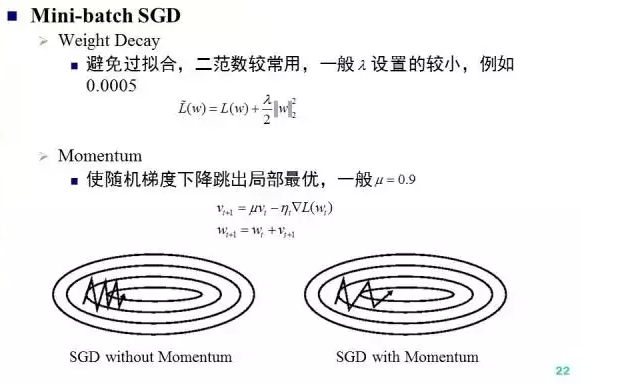
进一步的,在Mini-batch SGD中,有两个关键技术细节:weight decay和momentum. Weight decay是一种避免过拟合的正则化手段,而Momentum通过对历史梯度的moving average来避免陷入局部最优。
学习率
Learning rate即梯度下降的步长,是控制是网络收敛的关键,Caffe中支持四种策略,其中使用较多的是step和polynomial。
DL的2个问题
梯度消失
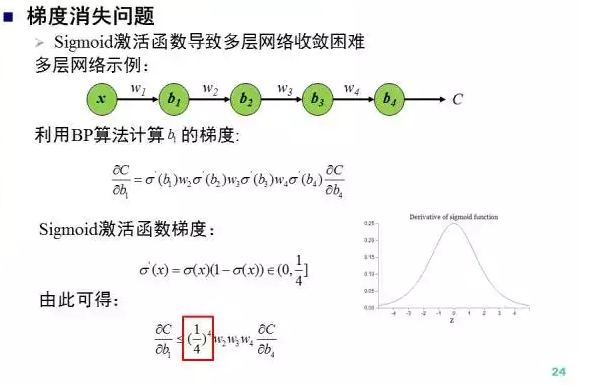
首先是梯度消失,梯度消失的主要原因是sigmoid激活函数“糟糕”的解析性质,一阶梯度的取值范围是[0,1/4],梯度向下传导一次最少会减小1/4,随着深度的增加,梯度传导的过程中不断减小从而引发所谓的“梯度消失”问题。

为了解决梯度消失问题,学术界提出了多种策略,例如,LSTM中的选择性记忆和遗忘机制,Hinton等提出的无监督pre-train方法,新的激活函数ReLU, 辅助损失函数和Batch Normalization.
梯度溢出
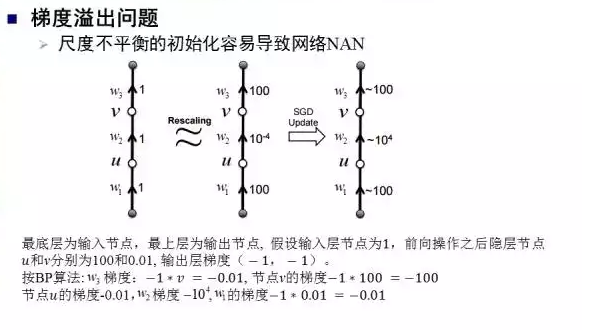
除了梯度消失之外,梯度溢出也是深度网络训练中的一个常见问题,例如Softmax损失变成86.33并且保持不变,这是因为梯度溢出导致网络参数NAN。梯度溢出的根本原因是网络参数初始化的尺度不平衡问题。上图中展示了一个例子,W2的初始值是0.01,梯度却达到10^4。

为了解决这个问题,Bengio等人提出了Xavier初始化策略,其基本思想是保持网络的尺度不变。
